Motion Planning Under Uncertainty for Planetary Navigation
NASA Jet Propulsion Laboratory
Robotics Research Deptartment - Autonomous Systems Division
Emilie Naples
University of California, Riverside
Department of Mathematics
NASA MIRO FIELDS Program
JPL Robotics Research Intern, Summer 2017
Autonomous Systems Division: Robotic Systems Section 347
Project Abstract:
During unmanned missions to space, it is critical for a machine to have the ability to operate without human assistance. A robot must operate autonomously in order to gather information about the unknown planetary body it intends to explore. When motion planning, a robot must be able to go from a start state to a goal state while accounting for the uncertainties in motion and
sensing. It must also be able to avoid any obstacles and calculate risk to determine the best path for doing so. We look for the most efficient way to accomplish this task and the path planning necessary to execute it. Simply put, we look at the problem of autonomous robotic planning and the implications caused by motion and sensing uncertainty.
The goal of this project was to enhance the Feedback Information Roadmap (FIRM) algorithm to account for both motion and sensing uncertainties to enhance motion planning capabilities for autonomous systems under extremely uncertain terrain and conditions. To approach this problem, I used POMDPs (Partially Observable Markov Decision Processes) as a way to maintain a sensor model, which represented the probability distribution of different observations in a robot’s environment. These observations are mapped to actions through a belief state which captures the robot’s knowledge about its surroundings. An exact solution to a POMDP then yields the optimal action for the robot over all states.
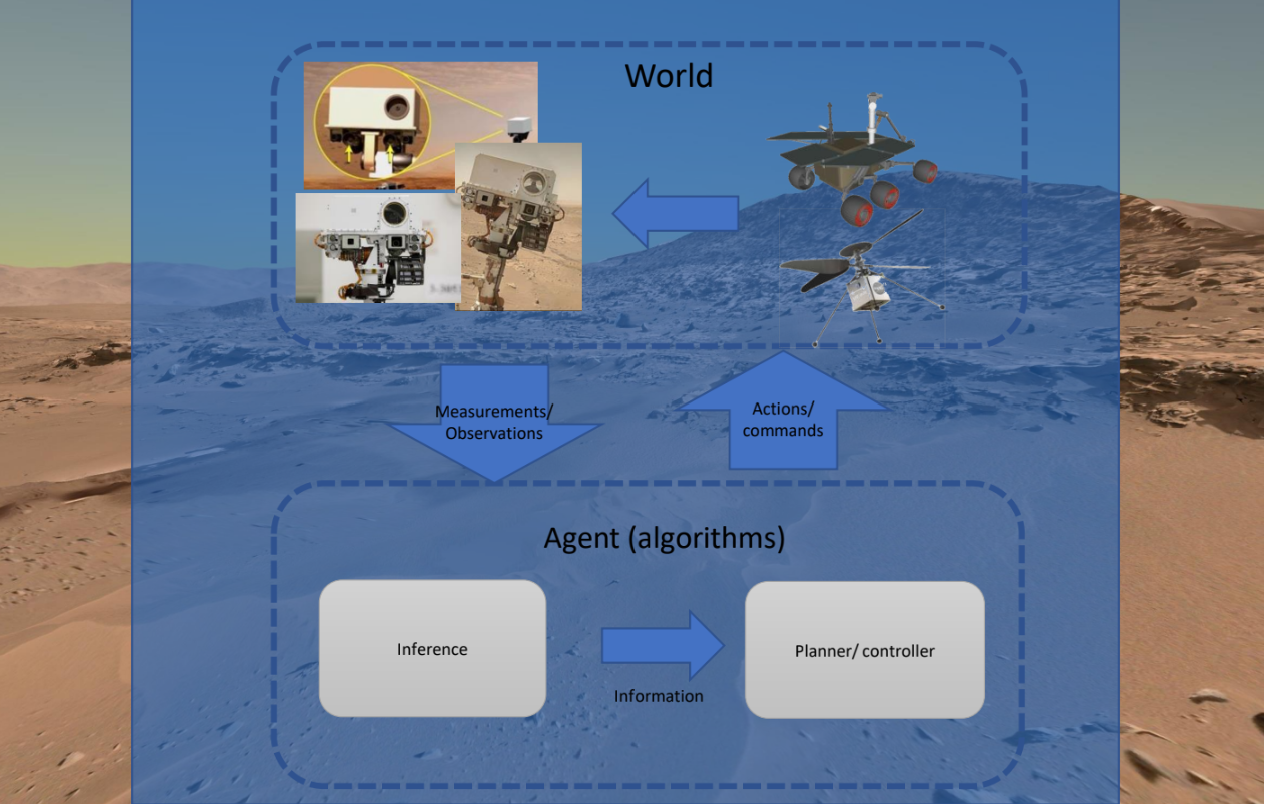
Problem:
Before, the algorithm only accounted for motion uncertainties. Decisions must be made about which action to take at each step or time point. The decision-maker or agent typically does not have full visibility of the true state of the environment (hence “partially observable”). Instead, they must rely on a set of observations that provide partial information about the state.
Goal:
Improve the algorithm (math side) to account for sensing (sight) & the dimensionality problem, thus addressing the challenges of motion and sensing uncertainties.
Solution:
Improve the FIRM algorithm (Feedback-based Information Roadmap) which updates the roadmap at each belief state. Doing so, the following improvements will be made:
- No need for expensive re-planning
- Still accounts for motion and sensing uncertainties
- Re-plans every time the localization module updates the probability distribution on the robot’s state
Significant Applications:
How were POMDPs applied to address path planning under extreme uncertainty?
By modeling the decision-making process as a partially observable environment:
- DEFINE THE STATES: Possible states of the environment, which include hidden information.
- DEFINE THE OBSERVATIONS: The noisy and incomplete data received from sensors.
- DEFINE THE ACTIONS: Possible movements and decisions the rover can take.
- DEFINE THE REWARDS: The system’s objectives, such as reaching a destination while avoiding obstacles.
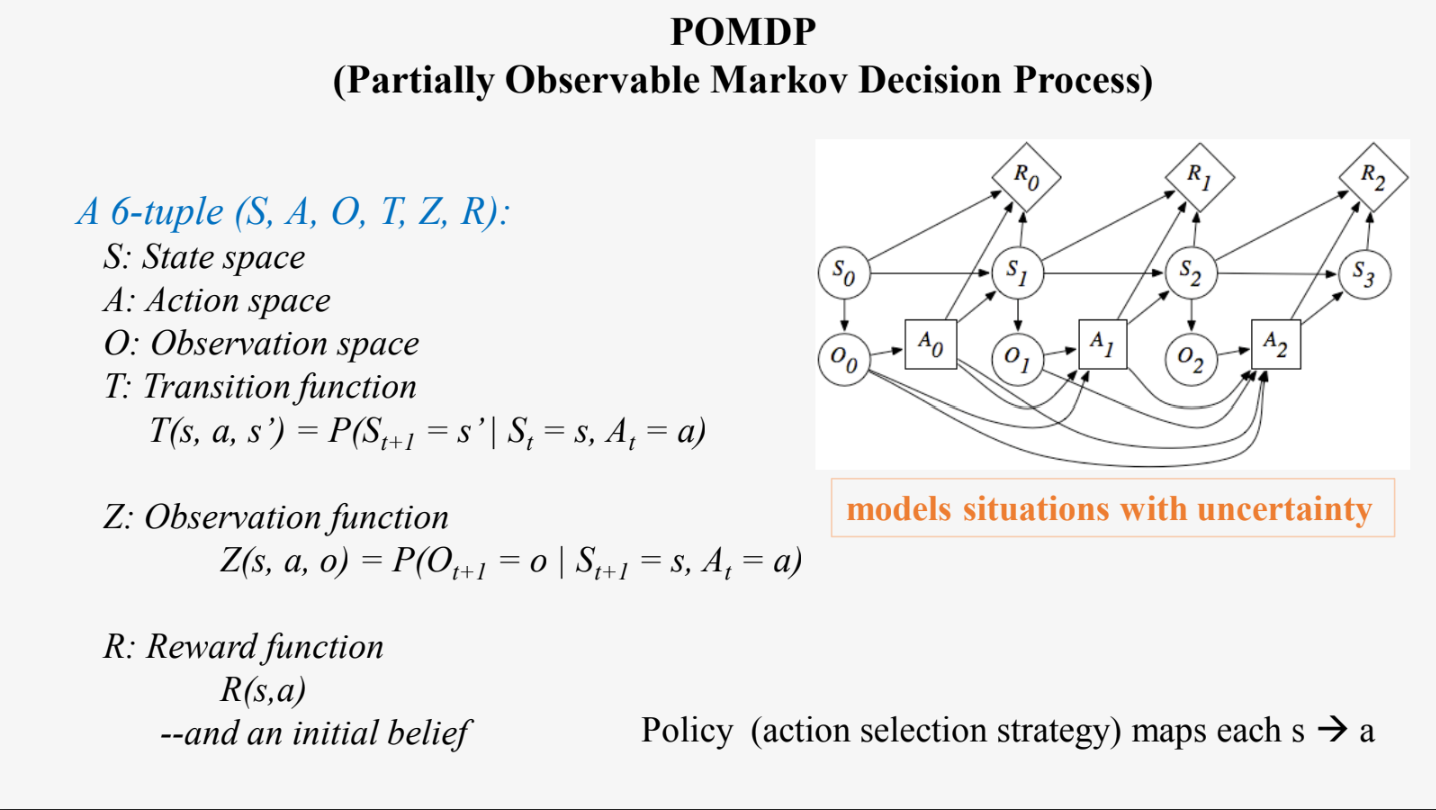
The POMDP is modeled as follows:
A 6-tuple (S, A, O, T, Z, R):
S: State space (set of all possible states the system can be in)
A: Action space ( set of all actions that the decision maker can take)
O: Observation space (set of all possible observations that the decision maker can make about the actual state of the system)
T: Transition function (deffines the probability of transitioning from one state to another state given a particular action) - T(s, a, s’) = P(St+1 = s’ | St = s, At = a)
Z: Observation function (gives the probability of making an observation given a state of the system and an action that has been taken).
Z(s, a, o) = P(Ot+1 = o | St+1 = s, At = a)
R(s, a): Reward function (assigns a numerical reward to each action taken in a particular state)
Additionally, a policy (action selection strategy) also defines the action to take in each state. The policy maps each
belief state s to an action → a.
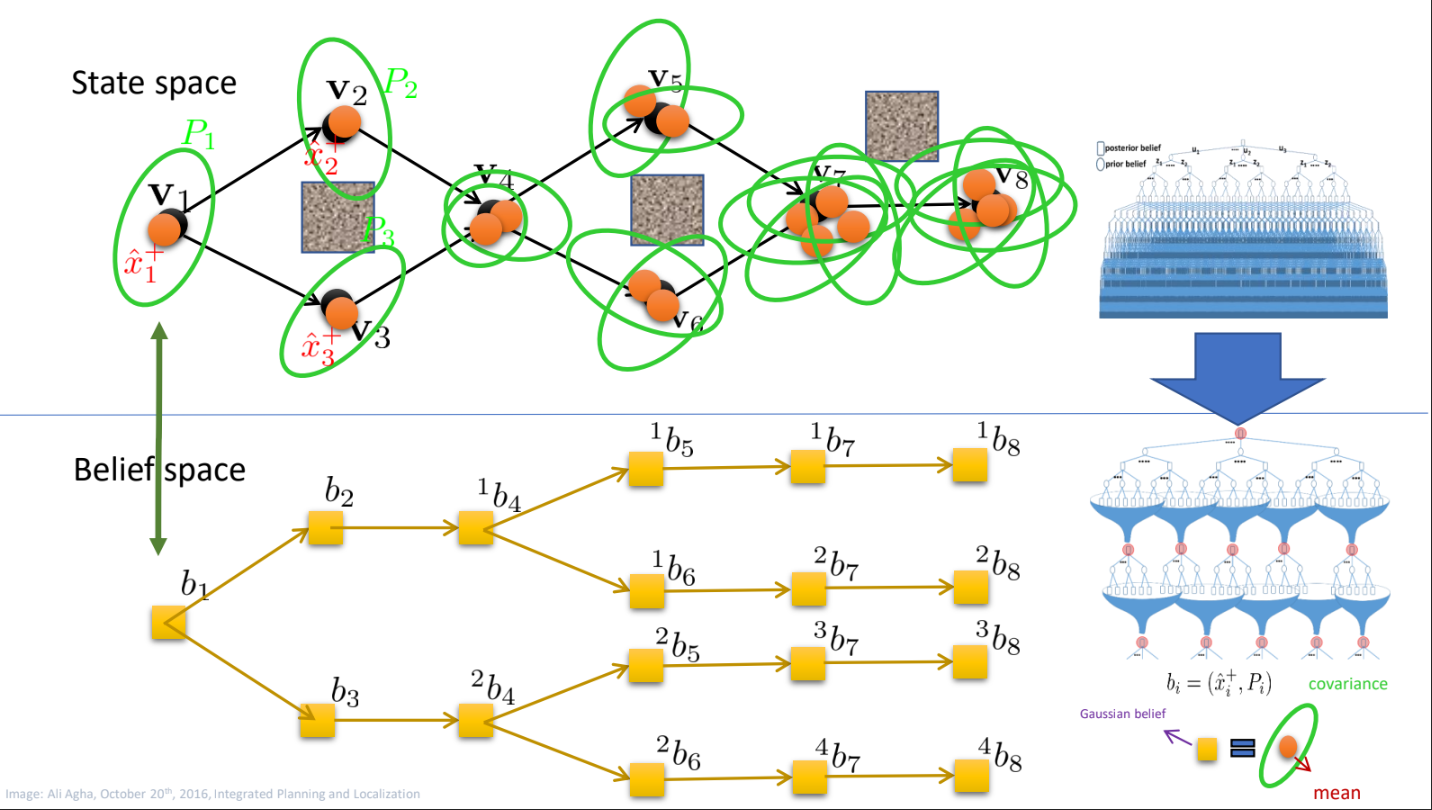
The progression of states (S0, S1, S2, etc.), observations (O0, O1, O2, etc.), actions (A0, A1, A2, etc.), and rewards (R0, R1, R2, etc.) over time. This kind of diagram is typically used to visualize the dynamics of a POMDP, where at each time step, an action is taken based on the current belief state, a new observation is made, and the belief state is updated.
We are then able to make decisions with incomplete knowledge about the current state and where the outcomes of actions are uncertain.